On the road to the Evaluation of Robustness of Reward Model
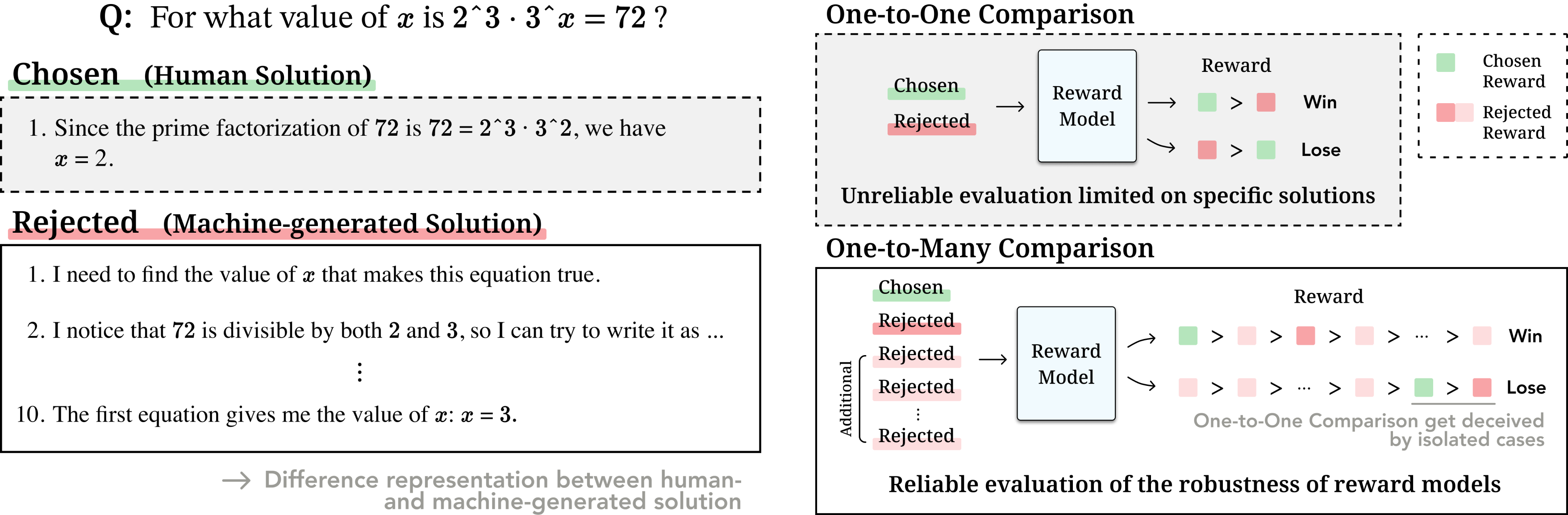
A motivation example from math subset of RewardBench and drawbacks of the existing evaluation method.
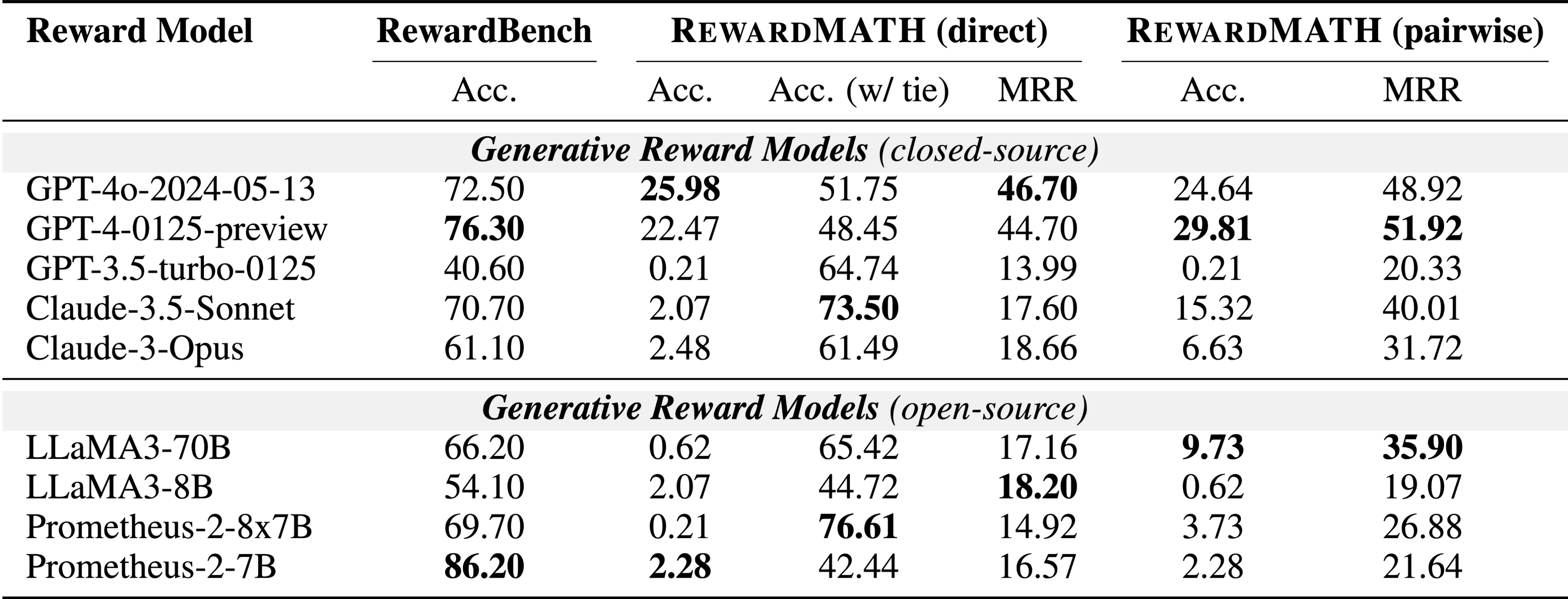
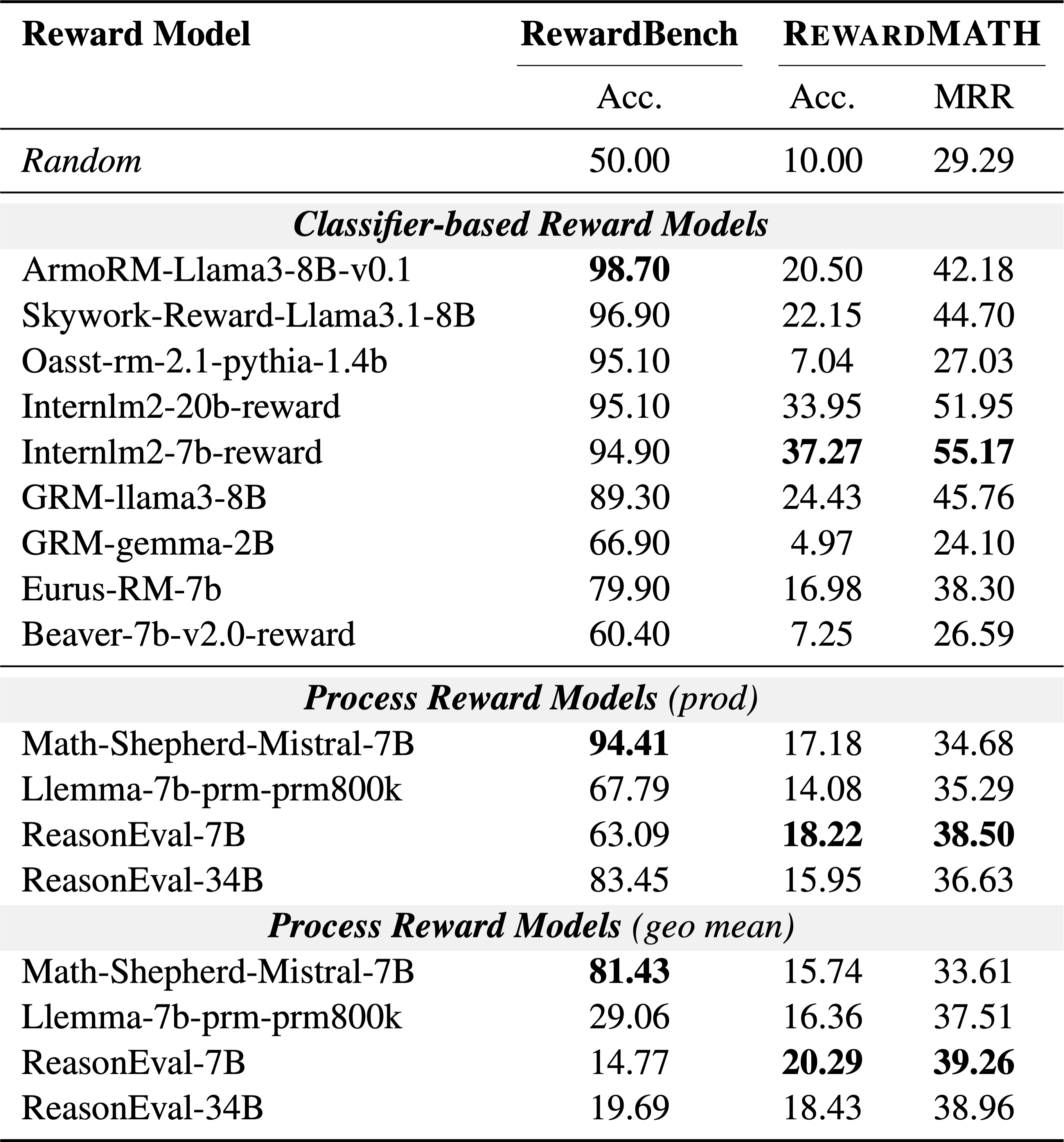
RewardBench, a widely-used benchmark for reward models, does not fully address the robustness of models in the math domain, with recent findings showing about 20% of the annotations in its underlying PRM800K dataset are incorrect. The evaluation process in RewardBench, which compares rewards between chosen and rejected solutions annotated by unaligned GPT-4, is flawed due to humans often skipping steps in solutions, leading to discrepancies with machine-generated solutions. These discrepancies challenge the evaluation’s reliability, as comparing with a single incorrect solution does not sufficiently assess the robustness of reward models.
RewardMATH
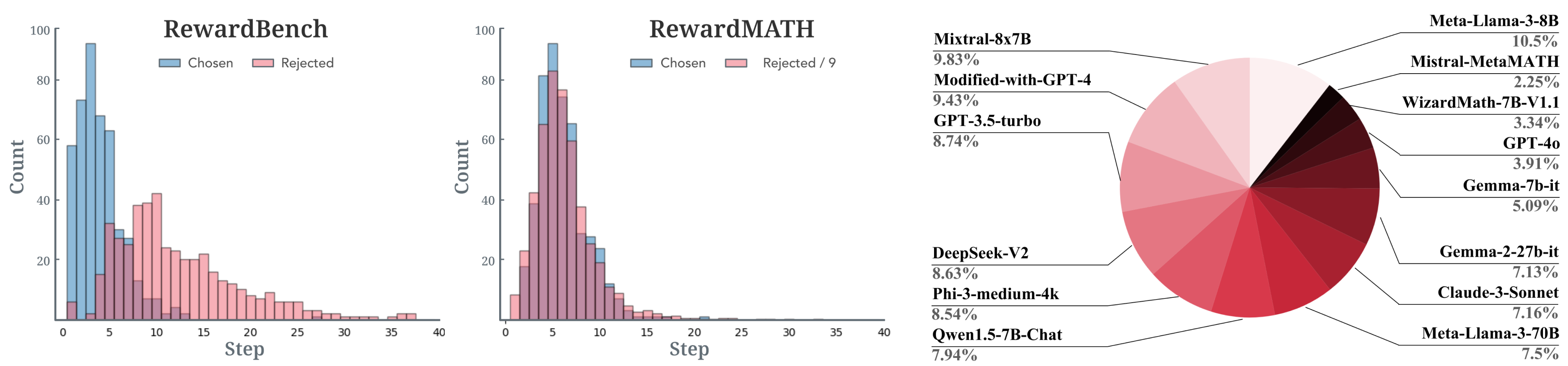
A histogram showing the distribution of samples by the number of steps on RewardBench and RewardMATH, and the contribution of each model to the rejected solutions.
The design philosophy of RewardMATH is to caution against a hasty generalization, which occurs when conclusions are drawn from a sample that is too small or consists of too few cases. To design a reliable benchmark, we aim to mitigate the risk of reward hacking and employs comparisons with a variety of incorrect (i.e., rejected) solutions. Therefore, we introduce RewardMATH, a reliable benchmark crafted for evaluating the robustness of reward models in mathematical reasoning.
Evaluation metric
For each problem, we infer 10 solutions in total—1 correct solution and 9 incorrect solutions—and then assign a true classification label when a reward of chosen solution is higher than all rewards of rejected solutions. Furthermore, considering only whether the reward of chosen solution is the highest can be fairly strict, we also utilize Mean Reciprocal Rank (MRR), where higher ranks for the chosen solution lead to higher scores.